Continua dalla pagina precedente

Il sistema di Eudosso, geniale per quanto riguarda la realizzazione, ma del tutto privo di un fondamento che potesse giustificare i valori dei raggi assegnati alle sfere, le loro velocità di rotazione e le inclinazioni dei loro assi, prevedeva quattro sfere per Mercurio, Venere, Marte, Giove e Saturno, tre sfere per il Sole e per la Luna e una sola sfera per le stelle fisse, il cui moto, del resto, era quello più semplice da riprodurre. Grazie a questo complesso sistema, fondato su ben 27 sfere, egli era riuscito a riprodurre discretamente bene, considerando anche i limiti di precisione delle osservazioni dell’epoca, soltanto i movimenti retrogradi di Giove e Saturno. Nel tentativo di migliorare l’accordo con le osservazioni, Callippo di Cizico, allievo di un allievo di Eudosso, aggiunse una sfera a Marte, Venere, Mercurio e alla Luna e due sfere al Sole. La sfera ulteriore per la Luna ne avrebbe dovuto riprodurre la variazione di velocità osservata che, come sappiamo oggi, è dovuta alla complessa interazione gravitazionale della Terra, del Sole e della Luna, mentre le due sfere aggiuntive per il Sole avrebbero dovuto riprodurre la diversa velocità orbitale annua apparente del Sole attorno alla Terra, per effetto della quale le stagioni hanno una durata diversa. La ragione di questa differenza è nota ormai da alcuni secoli e si deve al fatto che l’orbita della Terra attorno al Sole non è un cerchio, ma un’ellisse, il Sole non è al centro, ma in un fuoco di questa ellisse e la Terra si muove tanto più rapidamente quanto più è vicina al Sole: è più veloce, quindi, al perielio che all’afelio. Una velocità maggiore si traduce in un minor tempo di percorrenza e, poiché il periodo freddo per l’emisfero boreale corrisponde a una posizione della Terra più prossima al Sole di quanto sia per il periodo caldo, la stagione fredda, comprendente autunno e inverno, è più breve di circa sette giorni di quella calda, costituita da primavera ed estate. La situazione è inversa per l’emisfero australe.

Purtroppo, nonostante l’incremento da 27 a 33 del numero delle sfere, la modifica operata da Callippo non portò a ottenere alcun miglioramento significativo.
A noi, che conosciamo da molto tempo la realtà dei fatti, il sistema ideato da Eudosso risulta, oltre che artificioso, talmente assurdo che fatichiamo anche a comprenderne la ragione. Quale motivo poteva aver indotto Platone a desiderare tanto ardentemente che si potesse dimostrare che gli “evidenti movimenti” dei plànētes astéres derivavano da una combinazione di moti di sfere?

La sfera è indubbiamente il solido su cui ricadrebbe la scelta di chiunque volesse rappresentare geometricamente la perfezione. Non a caso, Parmenide, filosofo greco, vissuto circa un secolo prima di Eudosso, l’aveva identificata proprio con “l’essere” e Pitagora, contemporaneo di Parmenide, aveva nutrito una considerazione particolare per la sfera, in cui aveva colto l’armonia dell’ordine celeste, che si esemplificava attraverso il moto apparente notturno delle stelle. A tale proposito, è ancora Hermann Diels, nella Doxographi Graeci, ad attribuire ad Aezio l’affermazione che sarebbe stato proprio Pitagora a utilizzare per primo il termine Kósmos, parola che significava “ordine”, per indicare la sfera celeste, ossia la sfera immaginaria, di raggio indefinito, centrata sulla Terra sulla cui superficie appaiono proiettati tutti gli astri.

Il Cielo quindi, perfetto, puro e irraggiungibile dagli uomini, aveva avuto dalla divinità creatrice, il Demiurgo (seguendo Platone nel Timeo), una forma sferica, come appariva dal movimento ordinato delle stelle durante la notte e per questo motivo il sommo filosofo greco non riusciva a immaginare un moto celeste che potesse essere diverso da quello circolare uniforme e desiderava che gli “evidenti movimenti” dei pianeti dovessero essere ricondotti a un movimento di quel tipo: il loro disordine apparente doveva risultare, per forza di cose, dalla combinazione di moti circolari uniformi, che potevano avvenire soltanto lungo le sfere.

Aristotele che, per una serie di vicissitudini della storia, sarebbe risultato l’allievo più famoso di Platone, diede nel De Caelo, opera che scrisse intorno al 350 a.C., quella che ritenne la giustificazione fisica al moto delle innumerevoli sfere del sistema di Eudosso e di Callippo: era proprio l’ultima sfera, la più esterna e la più perfetta, quella delle “stelle fisse”, a essere in movimento e il suo moto veniva trasmesso via via verso l’interno a tutte le altre sfere. Per evitare, tuttavia, che la rotazione circolare e uniforme delle stelle lasciasse traccia di sé nel movimento osservato di ciascun pianeta, Aristotele doveva in qualche modo neutralizzarne l’effetto e così si era visto costretto ad aggiungere delle ulteriori sfere al modello di Eudosso e Callippo, portandole a un numero totale pari a 55, come afferma egli stesso nella Metaphysica.

Il “filosofo della natura” non parve nutrire alcun dubbio in relazione alla plausibilità di un modello così complicato e poco razionale – qual era il senso di un moto che doveva essere trasmesso e poi annullato? – né, tanto meno, della sostenibilità del suo modello in termini energetici: se un movimento veniva trasmesso e poi annullato, da dove si originavano tutti gli altri moti?

Il ragionamento lo aveva indotto a postulare, in accordo col suo maestro Platone, che l’Universo e i corpi celesti fossero costituiti da un elemento, “l’etere”, eterno, incorruttibile e privo di peso, a cui poteva competere soltanto il moto circolare uniforme. Gli altri quattro elementi, terra, acqua, aria e fuoco, che erano già patrimonio della tradizione pre-socratica, invece, popolavano la Terra e il mondo sublunare e si muovevano secondo traiettorie rettilinee, in direzione del loro luogo naturale.

Ad Aristotele mancava il concetto di forza e quindi era la natura stessa dei quattro elementi, la gravitas, maggiore per la terra che per l’acqua, e la levitas, minore per l’aria che per il fuoco, a indurli a muoversi verso il basso o verso l’alto. In questo modo, era riuscito a dar ragione sia del fatto che sulla Terra si trovavano i due elementi più pesanti, mentre i più leggeri stavano sopra di essa, sia dell’ordine con cui riteneva che gli elementi si disponessero nei loro luoghi naturali: la terra sotto l’acqua e il fuoco sopra l’aria.

Inoltre, era riuscito a liberarsi di un problema che aveva afflitto generazioni di studiosi dell’antichità e innumerevoli filosofi greci e riguardava il “sostegno” della Terra. Non era più necessario farla galleggiare sull’acqua, come aveva ipotizzato 300 anni prima Talete di Mileto, né sull’aria, come aveva sostenuto Anassimene, discepolo di Talete. La Terra, di forma sferica, era collocata esattamente al centro del Kósmos, la sfera dell’Universo, e non avrebbe potuto essere altrimenti, in quanto in qualunque altro luogo non sarebbe stata stabile. Oggi esprimeremmo questo concetto affermando che la Terra era per Aristotele nella “buca di potenziale” dell’Universo, ossia nel luogo in cui, se fosse stata spostata di poco, sarebbe andata naturalmente a ricadere: l’equidistanza da ogni “punto” della sfera dell’Universo era proprio la causa della sua stabilità.

Il ragionamento del filosofo greco non si arrestava qui, ma riusciva a fornire anche una motivazione per la forma della Terra: non esisteva, infatti, alcuna possibilità per l’elemento terra, attratto verso il suo luogo naturale, di distribuirsi in modo irregolare. Nonostante gli fosse sconosciuto il concetto di forza, quello che Aristotele era riuscito a esprimere col solo ausilio del suo ragionamento era proprio l’effetto che una forza centrale, ossia diretta come la congiungente tra il punto di applicazione e il centro (quale è la gravità), produce, generando corpi dotati di simmetria sferica.

Il modello di Aristotele continuava, evidentemente, a mostrare gli stessi problemi di cui aveva sofferto quello di Eudosso e Callippo, ovvero l’incapacità di riuscire a riprodurre, attraverso le combinazioni di moti circolari uniformi, i complessi movimenti mostrati dai pianeti.
Nel tentativo di migliorare l’accordo con le osservazioni, Apollonio di Perga, astronomo e matematico greco (di cui si sa pochissimo, se non che visse a cavallo fra il III e il II secolo a.C. in una cittadina situata in quella che oggi è la parte meridionale della Turchia e che si deve a lui la definizione delle coniche¹Dal Glossario: Coniche – Le figure geometriche, ellisse, circonferenza, parabola e iperbole, che risultano dall’intersezione di un piano, avente diverse inclinazioni, con un cono.), decise di dotare ciascun pianeta di due circonferenze di raggio diverso. Sulla più piccola, che chiamò “epiciclo”, o meglio epì-kyklos, ovvero cerchio – kyklos – che sta sopra – epì – collocò il pianeta e poi fece ruotare il centro dell’epiciclo lungo la circonferenza di raggio maggiore, a cui diede il nome di “deferente”. Entrambi i moti erano di tipo circolare uniforme e la loro combinazione riusciva a riprodurre i movimenti retrogradi dei pianeti (Fig. 4) con una precisione paragonabile a quella ottenuta col modello di Eudosso e Callippo.

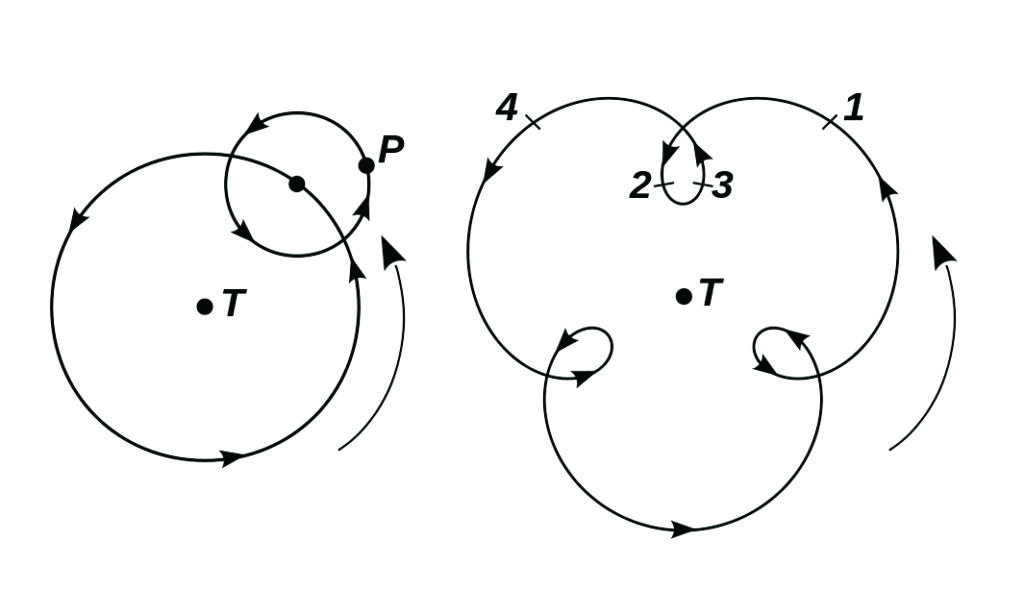
L’introduzione degli epicicli, tuttavia, aveva avuto un vantaggio non piccolo: muovendosi lungo di essi, i pianeti si avvicinavano e si allontanavano dalla Terra e questa variazione della distanza, non contemplata dal modello di Eudosso e Callippo, riusciva a dar ragione della variazione di luminosità osservata, perché a una minore distanza dalla Terra corrispondeva una maggiore luminosità del pianeta e viceversa. In realtà, come avrebbe mostrato Copernico, la variazione di luminosità si deve al fatto che, per effetto dei moti di rivoluzione della Terra e dei pianeti attorno al Sole, la distanza tra la Terra e i pianeti non è costante.

Ipparco di Nicea, matematico, geografo e astronomo greco, vissuto all’incirca un secolo dopo Apollonio, famoso per aver scoperto (dal confronto tra le posizioni delle stelle in cielo da lui osservate e quelle registrate dagli astronomi babilonesi alcune centinaia di anni prima) il fenomeno della precessione degli equinozi, decise di introdurre un artificio nel modello di Apollonio con l’obiettivo di riuscire a riprodurre la variazione di velocità angolare della Luna, del Sole e dei pianeti, osservata nel corso dell’anno, che la combinazione di moti circolari, di cui uno, quello sul deferente, centrato sulla Terra, non poteva rappresentare. L’idea di Ipparco fu di spostare il centro del deferente dalla Terra a un altro punto, l’eccentrico, in modo che il moto circolare uniforme del centro dell’epiciclo sul deferente non risultasse più tale, se visto dalla Terra.